Für dein Beispiel wäre [(p-n)/s] = [(4-2)/6] = 2/3, wie summiert man denn bis k=2/3 auf? Funktioniert das mit nicht-ganzzahligen Werten?
oh, ja, oben über der Summe steht die Zahl in Klammern. Das ist wohl eine floor-function oder auf deutsch eine Abrundungs-Funktion. Sie gibt die nächst mögliche ganzzahlige Zahl unterhalb des ergebnisses wieder
Also müsste man bei p=4 und n =2 und s=6 rechnen (4-2)/6 und auf 0 abrunden.
generell bei 2 Würfeln bei Summe zwischen 2-7 ist es 0 und bei Summe 8 bis 12 ist die floor function 1
und den Binomialausdruck kann man umformulieren
n über k ist gleich n!/k! (n-k)!
Ich versuche nachzudenken wie es denn bei einer Summe bis 0 funktioniert
Die eckigen Klammern, die nur unten einen Strich haben und oben offen sind, bedeuten ganzzahlig abrunden. Wären sie oben zu und unten offen, würde man aufrunden.
Ah ups, hab nicht so ganz genau hingeguckt und dachte das sind einfach normale eckige Klammern
Naja, die Summe bis Null wäre nur ein Term.
n über k ist dann 1, sieht man auch schön an deiner Fakultät-Schreibweise. 0! ist 1, n! kürzt sich weg.
bleibt noch p-1 über n-1, also 3 über 1, was dann 3!/2! = 3
(-1)^0 = 1
Bleibt 3/(6²) = 3/36 = 1/12
Ohne jetzt den Rest oben gelesen zu haben, ob das Ergebnis Sinn ergibt 
ah ich sehe. Irgendwie blackout gehabt
Aber nun selbst ausprobiert
Also die Formel ist dann folgende für 2 Würfel und natürlich 6 Seiten und wir interessieren uns für p=4 als Summe
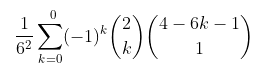
hinter dem Summenzeichen vereinfacht sich zu
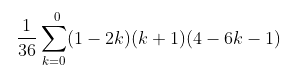
diesen Summen-Ausdruck dann z.B. hier berechnen Sigma (Sum) Calculator kommt 3 raus
1/36 * 3
= 3/36.
stimmt.
EDIT; und klappt auch bei beliebigen Zahlen z.B. Summe 17 bei 5 Würfeln (habe nun Wolfram rechnen lassen)
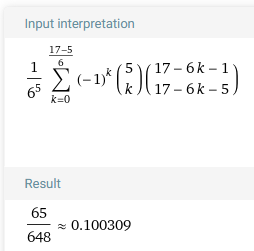
stimmt auch mit der manuellen Rechnung. Warum auch immer ich das gerade noch gerechnet habe 
Die Formel ist wohl nicht allzu sehr verbreitet und ist auf eine Quelle zurückzuführen, die man dank Gemeinfreiheit auch im Netz findet
Uspenski, 1937
Hier auch noch ein nettes Tool, bei dem schön sehen kann, dass mit mehr Würfeln die Wahrscheinlichkeit für eine bestimmte Summe allgemein sinkt
Und bei Gleichstand einfach nochmal würfeln ist keine Option? So lösen kleine Kinder das Problem jedenfalls. Wenn es aufgrund eines Gleichstands mehrere Sieger nach der ersten Runde gibt, würfeln diese nochmal. 
Aber theoretisch könnte so immer wieder ein Gleichstand kommen, bis die Kinder irgendwann mit 80 tot umfallen und sie das Spiel nie beenden konnten
Haben sie nicht gut durchdacht, die kleinen Kinder 
Solange sie dabei beschäftigt sind, sehe ich das als absoluten Gewinn. 
Aber besser wären sie dran mit meinen beiden Würfeln mit den Zahlen 1,3,5,6,8,10 und 2,4,4,7,7,9
Gewinnwslkeit von 50% und kein Gleichstand
Ach ja dieser Moment, wenn sich ein Thread wieder wie eine Vorlesung aus dem Studium anfühlt…
Auf jeden Fall sollten sie dann nebenbei auch Lotto spielen 
Es gibt auch noch mit 5 Würfeln würfeln, aber nur die geraden Zahlen zählen. Das habe ich weggelassen 
Wow. Das ist über meinen Schlaf ja ziemlich ausführlich geworden, hier.
Habe nicht viel hinzuzufügen.
Vielleicht für das zuletzt aufgezeigte Problem noch das hier:
tl;dw: Gibt ein Set Würfel, die alle verschiedene Zahlen haben, somit gibt es keinen Gleichstand. Außerdem sind die paarweise fair, d.h., es wird kein Würfel im „Gewinnen“ bevorzugt.
Kann man kaufen ![]()
Abgesehen von Würfeln gibt es natürlich andere Möglichkeiten, die Startreihenfolge festzulegen: Streichhölzer ziehen oder Umschläge mit verschiedenen Zahlen drin…
Wusste ich doch, dass ich solche Würfel schonmal irgendwo gesehen hab
Hab nur nix bei Google gefunden
Also ich bleib bei Ene mene muh
Spielst du Pen and Paper oder warum die Frage?
ah, seh grad erst: du hast oben ja auch schon einen Vorschlag gemacht für 2 verschiedene Würfel. Hattest du die selbst erdacht oder woher?

 ich liebs
ich liebs