Ich gehe mal davon aus, dass die meisten Läden nur innerhslb eines bestimmten Radius liefern und es daher stark davon abhängt, wo in Essen du wohnst.
Die Bewertungen bei Lieferando sind nicht hilfreich?
1 „Gefällt mir“
Leider nicht wirklich. Hatten 4,7 Bewertungen, 3,7 usw. Sind aktuell so 5-6 Restaurants die wir ausprobiert haben die alle nicht das wahre waren. Wenn du willst kann ich auch natürlich dir privat meine Adresse geben damit wir nen guten Laden finden
Echt witzig das er sowas ausspuckt 
Ich glaub nicht, dassich dane große Hilfe wäre 
ich würd halt nach Kategorien filtern (also Pasta) und dann schsuen, was es da so gibt. Vermutlich muss man halt wirklich durchprobieren.
Ich find Pasta im Restaurant (egal ob vor Ort oder bestellt) aber eh nie sehr prickelnd
1 „Gefällt mir“
Ah ok. Danke dir trotzdem für die Hilfe.
Hast du Chat GPT danach gefragt? Das hat doch nur einen Datensatz bis Ende 2021, ist also für sowas nur bedingt geeignet.
Nein, Bing.
3 „Gefällt mir“
Nutzt das nicht auch GPT-3?
- Next-generation OpenAI model . We’re excited to announce the new Bing is running on a new, next-generation OpenAI large language model that is more powerful than ChatGPT and customized specifically for search. It takes key learnings and advancements from ChatGPT and GPT-3.5 – and it is even faster, more accurate and more capable.
1 „Gefällt mir“
Ist arcsin(x) dasselbe wie sin^-1? Ich find sogar mit Google grade nix brauchbares
Der arcsin(x) wird ständig als Umkehrfunktion von sin(x) bezeichnet, mein Taschenrechner hat aber nur die Funktion „sin^-1“ und wenn ich bspw. eingebe sin^-1(sin(5)) erhalte ich als Ergebnis 5, also quasi die Umkehrfunktion.
Sind die beiden Sachen jetzt dasselbe? 
chatGPT sagt ja
Ja, arcsin(x) und sin^-1(x) bezeichnen beide die Umkehrfunktion der Sinusfunktion, die den Wert x annimmt. Beide Notationen werden oft synonym verwendet.
das ist aber Quatsch, ChatGPT.
Sie nimmt nicht den Wert x an sondern einen Wert (meinetwegen nenne man ihn y) an der Stelle x .
Ist natürlich Definitionssache aber ich würde ein f^-1 jetzt auch als Umkehrfunktion deuten.
Sollte dann also mit arcsin übereinstimmen, ja.
Ja das ist dasselbe
Die Funktionen Arkussinus, Arkuskosinus und Arkustangens (gebräuchlich sind die Bezeichnungen arcsin, sin^−1, asin) sind die Umkehrfunktionen der trigonometrischen Funktionen Sinus, Kosinus und Tangens
Aber Achtung sin^-1 (x) ungleich 1/sin(x)
2 „Gefällt mir“
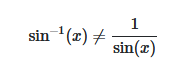
guter Hinweis.
das ist tatsächlich irreführend.
Also rein von der Notation her, da schreibt man ja x^-1 und meint 1/x
edit. Stelle ich mir bei Substitutionen sehr verwirrend vor
ja, das ist bei solchen Funktionen immer schwieriger zu verstehen.
Das hab ich sogar getestet und selbst rausgefunden 
Aber danke euch. Ich hoffe ich werde dieses Wissen niemals brauchen.
och. „brauchen“ tut man das eigentlich kaum, stimmt. aber ich finde sowas trotzdem sehr interessant und „gut zu wissen“.
Man möchte meinen das mathematische Notation uneindeutig und kontextabhängig ist und deshalb überholt werden sollte 
1 „Gefällt mir“
Herr Hilbert, sind Sie es? 
Bin dabei und reformiere gerne mit.
Wobei man das ja bei der allgemeinen Variante f^-1(x) auch hat. Deswegen lieber immer ein Paar Klammern zu viel als zu wenig 
Bei (sin(x))^-1 dürfte die Sache klar sein.
War gerade am Überlegen, ob die Alternative f quer besser wäre, aber da hat man dann das Problem mit der Doppeldeutigkeit der komplexen Konjugation 