Ohne eine einzige Rechnung zu rechnen würde ich intuitiv vermuten, dass es mit 5 Würfeln weniger wahrscheinlich ist. Je mehr Würfel man hat, desto mehr wahrscheinliche Summen werden möglich und desto kleiner sollten dann auch die Wahrscheinlichkeiten für bestimmte Summen werden
Aber je mehr Würfel ich würfele, umso eher stellt sich der Erwartungswert als ein Vielfaches von 3,5 ein.
Ein etwas praxisorientierter Ansatz:
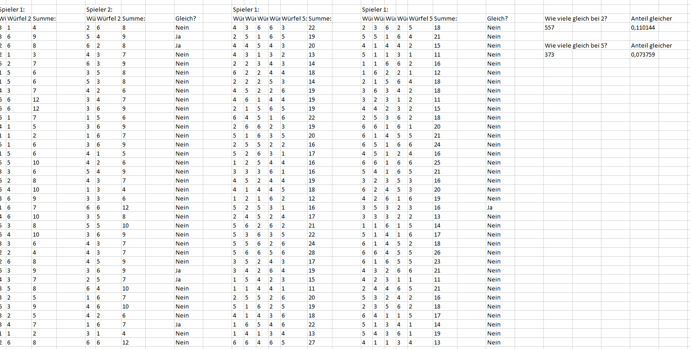
Ich habe jetzt Excel 5000 mal gegeneinander würfeln lassen, jeweils mit 2 und jeweils mit 5 Würfeln, dann hab ich zählen lassen, wie oft die Würfe gleich sind 
Und bei 2 Würfeln sind es jedes mal mehr gleiche

Bei 2 Würfeln sind es jedes mal etwa 11% Gleiche, bei 5 nur etwa 7%
Also herzer.
Die Wahrscheinlichkeit dass man mit einem Würfel eine 4 wirft ist 1/6. Die Wahrscheinlichkeit dass jemand anderes gleich danach eine 4 wirft ist auch 1/6. Aber die Wahrscheinlichkeit dass bei abhängiger Betrachtung die selbe Zahl geworfen wird ist 1/36.
Aber was ist wenn uns egal ist welche Zahl gleich zweimal nacheinander doppelt geworfen wird. Dann müssen wir alle Wahrscheinlichkeiten aufsummieren.
Die Wahrscheinlichkeit mit einem Würfel nacheinander die gleiche Augenzahl zu haben ist 1/6 (einfach die Einzelereignisse aufsummiert.)
Nun willst du das ganze für zwei Würfel wissen. Es gibt also 36 Möglichkeiten (6*6). Aber es gibt nur 11 verschiedene Summen (man kan ja keine 1 Würfeln)
Aber Achtung, ich hatte hier kurz auch etwas gelesen was nicht hinkommt. Die Wahrscheinlichkeit für z.B. Summe 7 ist nicht gleich 1/36, sondern 6/36 da es 6 Wege gibt eine 7 zu würfeln. Z.B. 2+5 oder 3+4 oder 5+2 (weil da muss man ja Würfel 1 und 2 Unterscheiden). Also sind die Einzelwahrscheinlichkeiten verschieden gewichtet.
Nun summiert man diese auf
Summe 2: (1/36) * (1/36) = 1/1296
Summe 3: (2/36) * (2/36) = 4/1296
Summe 4: (3/36) * (3/36) = 9/1296
Summe 5: (4/36) * (4/36) = 16/1296
Summe 6: (5/36) * (5/36) = 25/1296
Summe 7: (6/36) * (6/36) = 36/1296
Summe 8: (5/36) * (5/36) = 25/1296
Summe 9: (4/36) * (4/36) = 16/1296
Summe 10: (3/36) * (3/36) = 9/1296
Summe 11: (2/36) * (2/36) = 4/1296
Summe 12: (1/36) * (1/36) = 1/1296
Gesamtsumme:
macht am Ende eine Wahrscheinlichkeit von 146/1296 (einfach 1/1296+4/1296 …)
Und noch komplexer wird es bei 5 Würfeln. Zwar rangiert es von Summe 5 bis Summe 30. Aber die verschiedenen Summen sind krass anders gewichtet.
Nun folgt was vielleicht jemand bestätigen oder widerlegen könnte. Falls ich mich nicht verrechnet habe gibt es 540 Möglichkeiten eine 15 zu würfeln.
Rechnet man die Summe aller Möglichkeiten auf so kommt man auf 4395456/60466176 = 0,072692773.
da 0,112 (146/1296) größer ist, ist die Wahrscheinlichkeit mit 2 Würfeln die gleiche Summe zu würfeln größer als mit 5 Würfeln.
EDIT: Die Wahrscheinlichkeit mit 3 Würfeln die selbe Summe zu würfeln liegt bei 0,928. Bei 6 Würfeln liegt sie bei 0,0665. Sie sinkt also mit jedem Würfel leicht.
Wenn ihr also die selbe Summe vermeiden wollt. Weil 11% sind ja doch mehr als man vielleicht denkt, dann nehmt umso mehr Würfel
Ich hab jetzt ein Skript jeweils 200.000 mal gegeneinander würfeln lassen mit verschieden vielen Würfen, die Wahrscheinlichkeit eines Gleichstandes sinkt immer langsamer und nähert sich wahrscheinlich dem Grenzwert 0 bei unendlich Würfeln
@Herzer Wenn ihr wirklich sicher gehen wollt nehmt vielleicht einfach unendlich Würfel
Mich interessiert ja nicht die summe sondern nur das von ich bei 4 würfeln (2 personen je 2 würfel) ledilgich 2 unterschiedliche zahlen habe.
Dann wäre doch:
- würfel ergebnis egal = 6/6
- würfel ergebnis egal = 6/6
- würfel ergebnis eingeschränkt 2/6 (ich muss ja entweder das ergebnis von wurf 1 oder 2 treffen)
- noch weiter eingeschränkt 1/6 (ich muss das andere ergebnis von wurf 1 oder 2 treffen)
und das multiplizier ich einfach miteinander und nehme es mal 2 weil die reihenfolge egal ist
nachtrag: bei 5 würfeln ist die wahrscheinlichste zahl die gewürfelt wird die 17 und 18 mit gleicher wahrscheinlihckeit von 10.0309% (für 1 person)
Ich kann dir wirklich nicht folgen, kann es sein, dass beim ersten Satz etwas schiefgelaufen ist?
ich habs mal bearbeitet, mir gehts v.a. drum das ich der meinung bin das die summe und die wahrscheinlichkeit für das erreichen der summe egal ist.
Außer ich verstand die ausgangsfrage falsch, ich verstehe sie so:
Vulpaex wirft mit 2 würfeln eine 7, wie hoch ist die Wahrscheinlichkeit das Nesis90 mit 2 würfeln ebenfalls eine 7 würfelt. Ist die Wahrscheinlichkeit mit 5 würfeln größer oder kleiner, das Nesis die selbe summe wie Vulpaex würfelt.
Die Summe ist hier egal
aber sieh dir mal erstmal die Variante an mit 2 Würfeln nacheinander.
Eine Summe 4 zu würfeln kann man auf 3 Art (2,2) (3,1), (1,3). Also ist die Wahrscheinlichkeit eine 4 zu Würfeln 3/36.
Dasselbe gilt auch für den zweiten Wurf mit zwei Würfeln. Auch 3/36. Und dann multipliziert man das um die Wahrscheinlichkeit zu erhalten dass wir zwei mal dieselbe Zahl haben.
Aber das reicht noch nicht. Wir schauen ja nicht bloß auf Summe 4, sondern auf alle Summen. Man muss alle Wahrscheinlichkeiten addieren. (siehe Rechnung von mir oben)
Und ja du könntest auch mit 4 Würfeln rechnen, wobei das viel komplizierter wird, da die gleiche Augensumme nur mit geraden Zahlen gemacht wird. (wenn vorhin eine 4 gewürfelt wurde und im zweiten Wurf auch eine 4, dann macht das zusammen eine 8 mit 4 Würfeln). Dann fallen aber die Ereignisse mit ungeraden Zahlen weg und dann muss man das auch noch addieren. Ich glaube mit deiner Art ginge es, aber es ist noch viel komplexer.
Oder ich übersehe eine Methode wie man so ganz simpel auf 146/1296 kommt.
Die Wahrscheinlichkeit wenn du nur für den zweiten Wurf auf die 7 prüfst liegt bei 1/6, da mit 2 Würfeln bei 6 von 36 Optionen eine 7 raus kommt.
Willst du aber die Wahrscheinlichkeit vor dem ersten Wurf berechnen, liegt die Wahrscheinlichkeit bei (6/36)²+2*(5/36)²+2*(4/36)²…=0,112654. Die Wahrscheinlichkeit die gleiche Summe zu würfeln bei einer der anderen Optionen von 2 bis 12 nimmt immer weiter ab. Da gibt es sicher ne schöne mathematische Formel, mit der man sowas leicht berechnen kann.
Bisher gabe es nur ne Excel für Fließige ![]()
Dass du Formel haben möchtest hattest du nicht erwähnt, daran soll es nicht scheitern.
Bitte beim berechnen der Formel aufnehmen  da will ich sehen wie das jemand ausrechnet
da will ich sehen wie das jemand ausrechnet
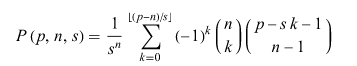
wobei p ist die gewünschte Summe (z.B. 4), n die Anzahl Würfel (z.B. 2) und s die Anzahl an Seiten (normaler Würfel mit 6 Seiten)
Das Ergebnis für jede Summe ist dann so etwas
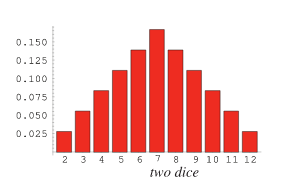
(Das ist die Formel die Bolthier meinte wie ich das verstanden habe, also für eine bestimmte Anzahl an Würfeln eine Summe)
Für dein Beispiel wäre [(p-n)/s] = [(4-2)/6] = 2/3, wie summiert man denn bis k=2/3 auf? Funktioniert das mit nicht-ganzzahligen Werten?
oh, ja, oben über der Summe steht die Zahl in Klammern. Das ist wohl eine floor-function oder auf deutsch eine Abrundungs-Funktion. Sie gibt die nächst mögliche ganzzahlige Zahl unterhalb des ergebnisses wieder
Also müsste man bei p=4 und n =2 und s=6 rechnen (4-2)/6 und auf 0 abrunden.
generell bei 2 Würfeln bei Summe zwischen 2-7 ist es 0 und bei Summe 8 bis 12 ist die floor function 1
und den Binomialausdruck kann man umformulieren
n über k ist gleich n!/k! (n-k)!
Ich versuche nachzudenken wie es denn bei einer Summe bis 0 funktioniert
Die eckigen Klammern, die nur unten einen Strich haben und oben offen sind, bedeuten ganzzahlig abrunden. Wären sie oben zu und unten offen, würde man aufrunden.
Ah ups, hab nicht so ganz genau hingeguckt und dachte das sind einfach normale eckige Klammern
Naja, die Summe bis Null wäre nur ein Term.
n über k ist dann 1, sieht man auch schön an deiner Fakultät-Schreibweise. 0! ist 1, n! kürzt sich weg.
bleibt noch p-1 über n-1, also 3 über 1, was dann 3!/2! = 3
(-1)^0 = 1
Bleibt 3/(6²) = 3/36 = 1/12
Ohne jetzt den Rest oben gelesen zu haben, ob das Ergebnis Sinn ergibt 
ah ich sehe. Irgendwie blackout gehabt
Aber nun selbst ausprobiert
Also die Formel ist dann folgende für 2 Würfel und natürlich 6 Seiten und wir interessieren uns für p=4 als Summe
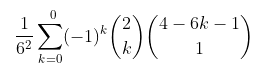
hinter dem Summenzeichen vereinfacht sich zu
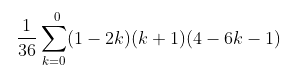
diesen Summen-Ausdruck dann z.B. hier berechnen Sigma (Sum) Calculator kommt 3 raus
1/36 * 3
= 3/36.
stimmt.
EDIT; und klappt auch bei beliebigen Zahlen z.B. Summe 17 bei 5 Würfeln (habe nun Wolfram rechnen lassen)
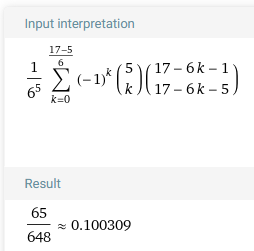
stimmt auch mit der manuellen Rechnung. Warum auch immer ich das gerade noch gerechnet habe 
Die Formel ist wohl nicht allzu sehr verbreitet und ist auf eine Quelle zurückzuführen, die man dank Gemeinfreiheit auch im Netz findet
Uspenski, 1937
Hier auch noch ein nettes Tool, bei dem schön sehen kann, dass mit mehr Würfeln die Wahrscheinlichkeit für eine bestimmte Summe allgemein sinkt
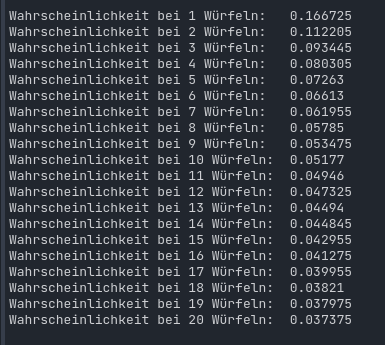
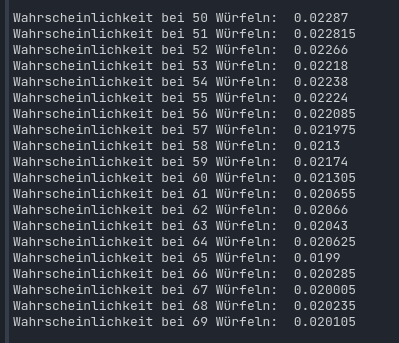

 ich liebs
ich liebs