da hast du recht.
Denke, meine interne Verwirrung kommt daher, dass ich gar nicht mit den Radi der Gefäße gerechnet habe sondern mit denen der Pudding-Oberfläche. Die ist ja (nach dem Umfüllen) bekannt und kann gemessen werden.
Wenn man aber vor dem Umfüllen wissen will, ob es sich lohnt (=mehr Haut), dann müsste man das Volumen (und damit die Füllhöhe und damit die Fläche) vorher berechnen. Ok, gut, danke!
Volumen einer halb-vollen Schüssel ist übrigens pi/3*(3r-h)h^2, wobei r der Radius der Schüssel ist und h die Füllhöhe. Die Luftfläche ist pisqrt(2r*h-h^2).
Jetzt muss man nur die Größen der Schüsseln und Töpfe finden und kann ausrechnen, was „besser“ ist.
1 „Gefällt mir“
Auf der Website hier kann man bekannte Zahlenreihen suchen, vielleicht wirst du da fündig: The On-Line Encyclopedia of Integer Sequences® (OEIS®)
Edit: Hier hab ich auch schon deine Zahlenreihe eingegeben: Da siehst du dann, welche Probleme alle durch die Zahlenreihe beschrieben werden:
https://oeis.org/search?q=21%2C+56%2C+126%2C+252&go=Search
1 „Gefällt mir“
bisher völlig an mir vorüber gegangen…
…mir wurde gerade nur ein React vorgeschlagen - ich verlink das mal - sehr schön:
1 „Gefällt mir“
Was ist das für ne Kurvenschar?
Die Achsenlabel verwirren mich etwas.
Dachte erst an x^x aber wieso ist es dann eine Schar? Was ist der zusätzliche Parameter für die einzelnen Kurven?
Btw find ich x^x ne sehr interessante Funktion.
Insbesondere der Lim gegen +0 und dann mit negativem, nicht-ganzzahligem x… …da wird es dann komplex.
1 „Gefällt mir“
Ich muss gestehen ich bin auch ein bisschen verwirrt und versuche gerade die Achsenlabel zu entschlüsseln.
Bis zu deinem Post kannte ich den Begriff Potenzturm nicht einmal… 
Die Schreibweise war mir bekannt, aber der Begriff war mir neu…^^
1 „Gefällt mir“
Hast du dich mal in das Rabbithole der Pfeilnotation und in dem Zusammenhang Grahams Zahl begeben?
Potenztürme sind nur der Anfang…
Die Achsen in deinem Graphen fangen ja irgendwie nicht bei 0|0 an sondern e scheint hier Grundlage der Definition zu sein und auch der Ursprung ist ja irgendwie bei 1/(e^e).
Vielleicht irgendwas Logarithmisches?
Es fällt jedenfalls auf, dass alle Kurven der Schar durch 1|1 gehen…
Was sagt Legolas zu Hawkeye?
„Immer einen Pfeil mehr als wie du!“
Glaube langsam wirklich Mathematiker müssen irgendwas kompensieren.
Aber Danke ich schau es mir mal in Ruhe an…will aber noch ein bisschen das Wetter nutzen.
Für alle a=n ist doch y(x)=x^x^x^x^x…n-mal oder?
dh y(1)=1^1^1^1^1^1…=1
Ja ist verwirrend…
1 „Gefällt mir“
Übersehe ich irgendwas? Aber wenn man doch auf das Bild klickt, sieht man in der Bildunterschrift auf Wikipedia ja doch, was das für eine Schar ist 
x↑↑a für a = 2,3,4,5,6,7 und Grenzwerte für a gegen unendlich (grau)
2 „Gefällt mir“
ja. ich war gar nicht auf der wiki page. jetzt schon - danke 
1 „Gefällt mir“
Weil dieser Thread viel zu leer ist…
Geometrische Verteilung / Harmonische Serie schön nerdig am Bsp. Pokemon erklärt.
Find den Mathe Prof sehr sympathisch.
3 „Gefällt mir“
hm.
is noch zu früh und mein Kopf zu matschig…
wir hatten 102 Tln bei der Monatsumfrage und 99 Tln bei der Tagesumfrage.
der Einfachheit könnte man auf 100 jeweils runden.
9/100 haben im Juli Geburtstag
8/100 an einem 12. eines beliebigen Monats.
Jetzt müsste man noch die Wahrscheinlichkeit rauskriegen, dass sich das überschneidet…
…da bin ich noch nicht fit genug und auch gerade zu faul…
…gebe das Zepter gerne hier weiter, wenn jemand seine/ihre Gedanken äußern möchte.
Edit… …ich vermute was mit bedingten Wahrscheinlichkeiten und irgendwas mit Bayes…
…aber nee… …erkältet denkt sich nicht so gut. Stochastik war für mich auch immer das ungeliebte Stiefkind der Mathewelt 
Stochastik ist halt auch doof.
Wir dürfen nicht ohne weiteres Unabhängigkeit von Tag/Monat annehmen. Grade die Nicht-Existenz eines 31.4 macht die Annahme schon zunichte.
Wenn wir das könnten, haben wir etwa 7 pro 1000 Leute, die am 12.7 geboren wurden. Bei absoluter Gleichverteilung 1/365 wären das 2.5 pro 1000.
korrekt
in einer Näherung vielleicht?
die Spanne 28.25 bis 31 ist immerhin nicht so super-riesig.
Die haben wir ja gerade nicht.
Die Umfrage zeigt schon deutliche Schwankungen und z.B. im Oktober haben nur 4% der abstimmenden User Geburtstag.
Was hast du gerechnet?
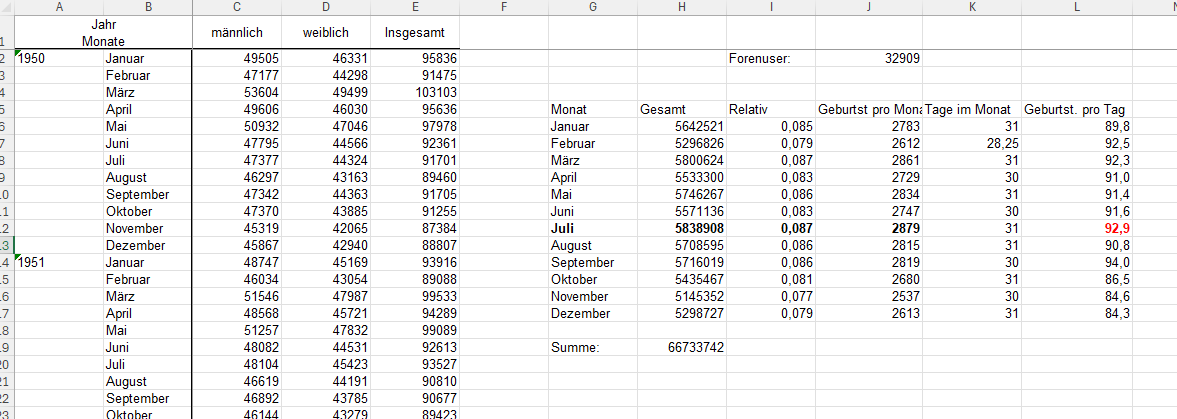
Ich hab mir die Geburtstatistiken pro Monat von 1950 - 2023 beim Statistischen Bundesamt runtergeladen und geguckt, wie sich die Geburtenzahlen über die Monate relativ verteilen.
Dann hab ich die Zahl genommen und als Faktor mit der Anzahl der Forenuser multipliziert um die Geburtstage pro Monat dann durch die Anzahl der Tage im Monat zu Teilen.
Im Juli haben täglich statistisch durchschnittlich 93 Accounts im Forum Geburtstag.
Alles gute.
Die Wahrscheinlichkeit an einem Tag niemand davon Geburtstag hat müsste (354/355)^32909 * 100% ≈ 5*10^-39 % sein. Angenommen das ist überhaupt die richtige Formel dafür und Schaltjahre ignoriert.
1 „Gefällt mir“
9/102 * 8/99.
Das ist P(Juli) * P(12.). Unter Annahme der Unabhängigkeit von Monat vs Tag kann man das so machen. Glaub ich…
1 „Gefällt mir“
Ist allerdings ziemlich ausgeschmückt.
(e+e)/e und e-e, also bitte 
Da fällt mir nur
zu ein.