Das ist der Code in C (ohne Bashscripting)
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
//Feste Systemparameter (nicht von Anwender manipulierbar)######################################################
#define m 0.01 // Masse der Kugeln in kg
#define L 8.0 // Länge der Pendel im Gravitationsfeld in cm
#define a 1.0 // Abstand der Ruhepositionen in cm
#define g 1000.0 // Gravitationsbeschleunigung in -y-Richtung in cm/s^2
#define k 1000.0 // Federkonstante in kg/s^2
#define L0 7.99 // Ruhelänge des Pedels im Gravitationsfeld in cm
#define x0 (-2.0) // x-Postion der 0. Kugel in cm
#define epsilon 10000.0 // Lenard-Jones-Parameter Epsilon in kgcm^2/s^2
#define sigma 0.9 // Lenard-Jones-Parameter Sigma in cm
#define t_end 10.0 // End-Zeit in s
//#############################################################################################################
// Funktion, die Abstand zwischen zwei Kugeln i,j misst---------------------------
double Abstand(double feld[][2][2], int i, int j ){
double Erg;
Erg = sqrt(pow(feld[i][0][0]-feld[j][0][0],2)+ pow(feld[i][1][0]-feld[j][1][0],2));
return Erg;
}//-------------------------------------------------------------------------------
//Länge der Feder-----------------------------------------------------------------
double Laenge(double feld[][2][2], int i){
double Erg;
Erg = sqrt(pow(feld[i][0][0]-ia,2)+pow(feld[i][1][0]-L,2));
return Erg;
}//------------------------------------------------------------------------------
//Kinetische Energie eines Teilchens i-------------------------------------------
double T_i(double feld[][2][2], int i){
double Erg;
Erg = 0.5m(pow(feld[i][0][1],2)+pow(feld[i][1][1],2));
return Erg;
}//------------------------------------------------------------------------------
//Potenzielle Energie eines Teilchens i ohne Lenard-Jones-Potenzial--------------
double V0_i(double feld[][2][2], int i){
double Erg;
Erg = 0.5kpow(Laenge(feld,i)-L0,2) + mgfeld[i][1][0];
return Erg;
}//------------------------------------------------------------------------------
//Lenard-Jones-Potenzial zwischen Teilchen i und j:-------------------------------
double VLJ_ij(double feld[][2][2], int i, int j){
double Erg;
if(Abstand(feld,i,j)<sigma && i!=j){
Erg = epsilon*(pow(sigma/Abstand(feld,i,j),12)-2pow(sigma/Abstand(feld,i,j),6)+1);
}else{
Erg = 0.0;
}
return Erg;
}
//Summe aller Lenard-Jones-Wechselwirkungen für ein Teilchen i-------------------
double VLJ_i(double feld[][2][2], int i, int N ){
double Erg=0.0;
int j;
for(j=0; j<N; j++){
Erg= Erg+ 0.5VLJ_ij(feld,i,j);
}
return Erg;
}
//Differentialgleichung für Teilchen i ohne Lenard-Jones-Potenzial…------------
//… für x-Komponente:+++++++++++++++++++++++++++++++++
double F0x_i(double feld[][2][2], int i){
double Erg;
Erg = -k/m*(Laenge(feld,i)-L0)(feld[i][0][0]-ia)/Laenge(feld,i);
return Erg;
}//+++++++++++++++++++++++++++++++++++++++++++++++++++++
//… für y-Komponente:+++++++++++++++++++++++++++++++++
double F0y_i(double feld[][2][2], int i){
double Erg;
Erg = -k/m*(Laenge(feld,i)-L0)(feld[i][1][0]-L)/Laenge(feld,i)-g;
return Erg;
}//+++++++++++++++++++++++++++++++++++++++++++++++++++++
//--------------------------------------------------------------------------------
//Differentialgleichung für Lenard-Jones-Wechselwirkung zwischen Teilchen i,j:----
double FLJ_ij(double feld[][2][2], int i, int j){
double Erg;
if(Abstand(feld,i,j)<sigma&&i!=j){
Erg = 12epsilon*(pow(sigma,6)pow(Abstand(feld,i,j),-7)-pow(sigma,12)pow(Abstand(feld,i,j),-13));
}else{
Erg = 0.0;
}
return Erg;
}
//Differentialgleichung für Lenard-Jones-Wechselwirkung für die beiden Komponenten:
//…x-Komponente:+++++++++++++++++++++++++++++++++++++++
double FLJx_i(double feld[][2][2], int i, int N){
double Erg = 0.0;
int j;
for(j=0; j<N; j++){
if(i!=j){
Erg = Erg -FLJ_ij(feld,i,j)(feld[i][0][0]-feld[j][0][0])/Abstand(feld,i,j);
}else{
Erg = Erg;
}
}
return Erg;
}//+++++++++++++++++++++++++++++++++++++++++++++++++++++++
//…y-Komponente:++++++++++++++++++++++++++++++++++++
double FLJy_i(double feld[][2][2], int i, int N ){
double Erg=0.0;
int j;
for(j=0; j<N; j++){
if(i!=j){
Erg = Erg - FLJ_ij(feld,i,j)(feld[i][1][0]-feld[j][1][0])/Abstand(feld,i,j);
}else{
Erg = Erg;
}
}
return Erg;
}
//gesamte Beschleunigungsterme+++++++++++++++++++++++++++++++++++++++++++++++
//…für x-Komponente
double Fx_i(double feld[][2][2], int i, int N){
double Erg;
Erg = F0x_i(feld,i) + 0.5/mFLJx_i(feld,i,N);
return Erg;
}//---------------------------------------------------
//für y-Komponente-------------------------------------
double Fy_i(double feld[][2][2], int i, int N){
double Erg;
Erg = F0y_i(feld,i) + 0.5/mFLJy_i(feld,i,N);
return Erg;
}//----------------------------------------------------
//+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
int main(int argc, char argv[]){
//Konfigurations-Array-------------------------------(erklären wies funktioniert
int N = 2;
//int N = atoi(argv[1]);// Teilchenanzahl aus Programmaufruf
//double dt = atof(argv[2]);// Zeitschrittweite aus Programmaufruf
int algorithm = 0;
double Sys_alt[N][2][2];// Systemkonfiguration erste Komponente = Teilchen, zweite Komponente = x oder y , dritte Komponente x oder x’
double Sys_neu[N][2][2];
int i,j,l;
//----------------------------------------------------------------------------
//Initialisieren des Konfigurations-Arrays#####################################################################
//Orte der 0. Kugel++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Sys_alt[0][0][0] = x0;
Sys_alt[0][1][0] = L-sqrt(pow(L,2)-pow(x0,2));
//+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
//Orte der anderen Kugeln +++++++++++++++++++++++++++++++++++++++++++++++++++++
for(i=1; i<N; i++){
Sys_alt[i][0][0]=ia;
Sys_alt[i][1][0]=0.0;
}
//+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
//Geschwindigkeiten aller Kugeln+++++++++++++++++++++++++++++++++++++++++++++++
for(i=0; i<N;i++){
Sys_alt[i][0][1]= 0.0;
Sys_alt[i][1][1]= 0.0;
}
//+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
//#############################################################################################################
if(algorithm == 0){
//Euler-Algorithmus############################################################################################
double t=0.0;
double dt=0.00001;
double KinEnerg, PotEnerg, GesEnerg;
//Output-Files für Koordinaten der Teilchen und für Energien des Systems+++++++
char File1[100];
char File2[100];
sprintf(File2,„Daten_Energie_Euler.txt“);
sprintf(File1,„Daten_Koord_Euler.txt“);
FILE *f1=fopen(File1, „w“);
FILE *f2 =fopen(File2, „w“);
//+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
//Zeitschleife+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
do{
//Ausgabe der Koordinaten----------------------------------
fprintf(f1, „#t=%.4lf\n“,t);
for(i = 0; i<N; i++){
fprintf(f1,"%.5lf\t", Sys_alt[i][0][0]);
fprintf(f1,"%.5lf\n", Sys_alt[i][1][0]);
}
fprintf(f1, „\n“);//Doppeltes Leerzeichen für Trennung der Blöcke
fprintf(f1, „\n“);//der einzelnen Zeitpunkte für Plotprogramm
//---------------------------------------------------------
//Berechnung der Energien----------------------------------
KinEnerg =0.0;
PotEnerg =0.0;
//Bestimmen der kinetischen und potentiellen Energie durch Summation über T_i und V_i
for(i=0; i<N; i++){
KinEnerg = KinEnerg+ T_i(Sys_alt,i);
PotEnerg = PotEnerg+ V0_i(Sys_alt,i)+VLJ_i(Sys_alt, i, N);
}
GesEnerg = KinEnerg +PotEnerg;
//Ausgabe der Energien des Gesamtsystems zu den verschiedenen Zeitpunkten
fprintf(f2, „%.4lf\t“, t);
fprintf(f2, „%.5lf\t“, KinEnerg);
fprintf(f2, „%.5lf\t“, PotEnerg);
fprintf(f2, „%.5lf\n“, GesEnerg);
//---------------------------------------------------------
//Euler-Integration für jedes der N Teilchen---------------
for(i=0; i< N; i++){
Sys_neu[i][0][1] = Sys_alt[i][0][1]+ Fy_i(Sys_alt,i,N)*dt;//Geschwindigkeit in x-Richtung
Sys_neu[i][1][1] = Sys_alt[i][1][1]+ Fy_i(Sys_alt,i,N)*dt;//Geschwindigkeit in y-Richtung
Sys_neu[i][0][0] = Sys_alt[i][0][0]+ (Sys_alt[i][0][1] + Fx_i(Sys_alt,i,N)*dt)*dt;//x-Koordinaten
Sys_neu[i][1][0] = Sys_alt[i][1][0]+ (Sys_alt[i][1][1] + Fy_i(Sys_alt,i,N)*dt)*dt;//y-Koordinaten
}
//---------------------------------------------------------
//Vertauschen der beiden Arrays----------------------------
for(i=0; i<N;i++){
for(j = 0; j< 2; j++){
for(l=0; l< 2; l++){
Sys_alt[i][j][l] = Sys_neu[i][j][l];
}
}
}
//---------------------------------------------------------
t = t+dt;
}while(t<=t_end);
//+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
//Schließen der Dateien in die Daten ausgegeben wurden
fclose(f1);
fclose(f2);
}//############################################################################################################
if(algorithm ==1){
//Velocity-Verlet-Algorithmus##################################################################################
double t=0.0;
double dt=0.0001;
double KinEnerg, PotEnerg, GesEnerg;
//Output-Files für Koordinaten der Teilchen und für Energien des Systems+++++++
char File1[100];
char File2[100];
sprintf(File2,„Daten_Energie_VVerlet.txt“);
sprintf(File1,„Daten_Koord_VVerlet.txt“);
FILE *f1=fopen(File1, „w“);
FILE f2 =fopen(File2, „w“);
//+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
//Zwischenspeicher für vx_i(t+1/2dt) und vy_i(t+1/2dt)
double Zwischen[N][2];
//Zeitschleife+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
do{
//Ausgabe der Koordinaten----------------------------------
fprintf(f1, „#t=%.4lf\n“,t);
for(i = 0; i<N; i++){
fprintf(f1,"%.5lf\t", Sys_alt[i][0][0]);
fprintf(f1,"%.5lf\n", Sys_alt[i][1][0]);
}
fprintf(f1, „\n“);//Doppeltes Leerzeichen für Trennung der Blöcke …
fprintf(f1, „\n“);//…der einzelnen Zeitpunkte für Plotprogramm
//---------------------------------------------------------
//Berechnung der Energien----------------------------------
KinEnerg =0.0;
PotEnerg =0.0;
//Bestimmen der kinetischen und potentiellen Energie durch Summation über T_i und V_i
for(i=0; i<N; i++){
KinEnerg = KinEnerg+ T_i(Sys_alt,i);
PotEnerg = PotEnerg+ V0_i(Sys_alt,i)+VLJ_i(Sys_alt, i, N);
}
GesEnerg = KinEnerg +PotEnerg;
//Ausgabe der Energien des Gesamtsystems zu den verschiedenen Zeitpunkten
fprintf(f2, „%.4lf\t“, t);
fprintf(f2, „%.5lf\t“, KinEnerg);
fprintf(f2, „%.5lf\t“, PotEnerg);
fprintf(f2, „%.5lf\n“, GesEnerg);
//---------------------------------------------------------
//Velocity-Verlet-Integration für jedes der N Teilchen-----
//Berechnen der Zwischengeschwindigkeiten…
for(i=0;i<N; i++){
Zwischen[i][0]=Sys_alt[i][0][1] + 0.5Fx_i(Sys_alt,i,N)dt;
Zwischen[i][1]=Sys_alt[i][1][1] + 0.5Fy_i(Sys_alt,i,N)*dt;
}
//…
//Berechnen der neuen Orte…
for(i=0;i<N;i++){
Sys_neu[i][0][0] = Sys_alt[i][0][0]+Zwischen[i][0]*dt;
Sys_neu[i][1][0] = Sys_alt[i][1][0]+Zwischen[i][1]dt;
}
//…
//neue Geschwindigkeiten…
for(i=0;i<N;i++){
Sys_neu[i][0][1] = Sys_alt[i][0][1] + 0.5(Fx_i(Sys_alt,i,N)+Fx_i(Sys_neu,i,N))dt;
Sys_neu[i][1][1] = Sys_alt[i][1][1] + 0.5(Fy_i(Sys_alt,i,N)+Fy_i(Sys_neu,i,N))*dt;
}
//…
//---------------------------------------------------------
//Vertauschen der beiden Arrays----------------------------
for(i=0; i<N;i++){
for(j = 0; j< 2; j++){
for(l=0; l< 2; l++){
Sys_alt[i][j][l] = Sys_neu[i][j][l];
}
}
}
//---------------------------------------------------------
t = t+dt;
}while(t<=t_end);
//+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
//Schließen der Dateien in die Daten ausgegeben wurden
fclose(f1);
fclose(f2);
}//############################################################################################################
return 0;
}

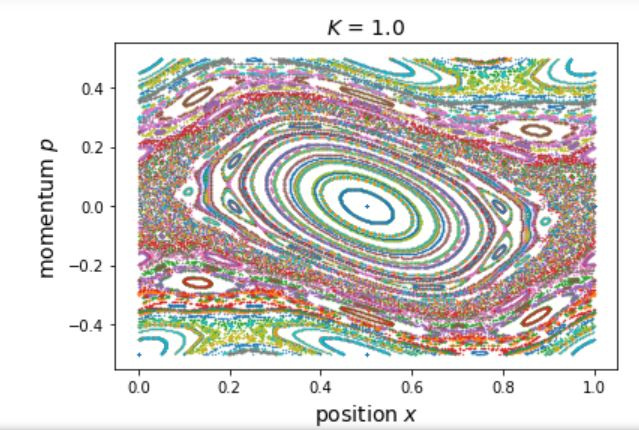






 /
/