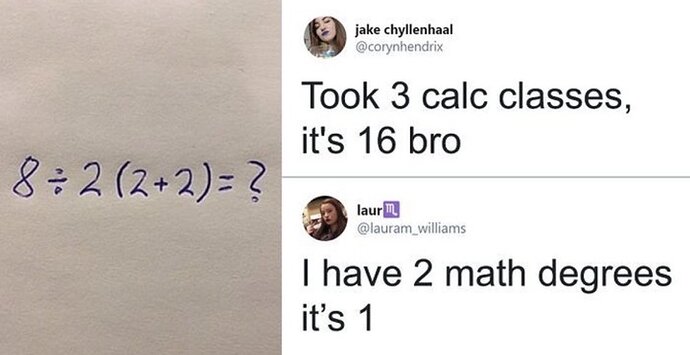Naja, wenn 200 Fisch-Doller 50ct (US) entspricht, dann 1 Fisch-Dollar = 0,25ct.
Bzw. 1 US-Dollar = 400 Fisch-Dollar 
2 „Gefällt mir“
Mit zwei Abschlüssen in Mathe sollte man eigentlich sehen, dass die aufgabe nicht eindeutig formuliert ist
1 „Gefällt mir“
Erst Klammern, dann Punktrechnung, dann Strichrechnung, Reihenfolge links nach rechts.
Hab auch ein Video über ein ähnliches Problem gesehen.
2 „Gefällt mir“
Damit wirst du auch zu zwei Ergebnissen kommen, je nach dem wie du die Gleichung definierst
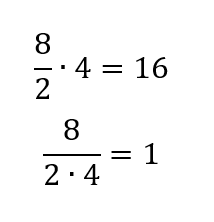
Es ist nicht erkennbar, ob die (2+2) noch zum Nenner gehören soll oder nicht
Dort steht aber kein Bruch. Dementsprechend gilt wie SilverMonkey sagt von links nach rechts und somit ist das Ergebnis eindeutig 16. Für die zweite Gleichung müsste die Originalaufgabe 8:(2(2+2)) lauten, was sie aber nicht tut.
Eine Division lässt sich immer mit einem Bruch ersetzen, da es sich um dieselbe Rechnungsart handelt, ist nur eine andere Darstellungsform.
2 „Gefällt mir“
wieso?
1 „Gefällt mir“
Das Ding ist, dass es für manche wohl die Regel gibt, wenn kein Mal vor der Klammer steht, gehören die beiden Terme zusammen (währen also im Nenner). Ist aber keine universelle Regel und Definitionssache der Notation.
Da es eben keine allgemeingültige Regel ist, bin ich auch für die strikte Rechnung von links nach rechts und das fehlende Mal denkt man sich wie üblich eben dazu.
Wer das Problem eindeutig für alle angeben mag, soll lieber ein Klammerpaar mehr setzen, als sich merkwürdige Notationsregeln auszudenken, die nicht von allen gleichermaßen akzeptiert werden 
Richtig, aber daraus kann man nicht wie Nesis90 annehmen, dass die (2+2) zu dem Nenner von 8 : … gehört.
Bzgl. @Squidward: Du kannst dir auch einfach merken, dass Punkt- vor Strichrechnung gilt und Multiplikation kommutativ ist, d.h. 8:2*(2+2) = 8*(2+2):2 = (2+2):2*8 = … = 16.
Wieso nicht? Ich sähe nix, was dagegen spräche.
Es hat schon seinen Grund warum außer kleinen Kindern niemand diese Schreibweise mit : benutzt.
4 „Gefällt mir“
Ja, aber du kannst nicht einfach implizit Klammern setzen. Da nicht noch ein Klammerpaar da ist nur der direkte Term hinter dem Divisionszeichen „unterm Bruch“.
Hatte es gerade auch mit meiner Freundin, dass der Bruchstrich besser weil wesentlich eindeutiger ist 
Das war nicht meine Frage, aber egal.
Jep, das Problem hier ist schlichtweg, dass die Aufgabe schlecht dargestellt ist.
1 „Gefällt mir“
Weil die Notation 2(2+2) für manche eine höhere Priorisierung in der Auflösung impliziert, als eine 2*(2+2), für manche nicht.
Es ist eben nicht eindeutig festgelegt. Dadurch kommt es erst zu diesem Problem.