Dass du Formel haben möchtest hattest du nicht erwähnt, daran soll es nicht scheitern.
Bitte beim berechnen der Formel aufnehmen 
da will ich sehen wie das jemand ausrechnet
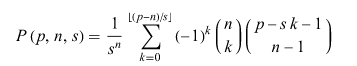
wobei p ist die gewünschte Summe (z.B. 4), n die Anzahl Würfel (z.B. 2) und s die Anzahl an Seiten (normaler Würfel mit 6 Seiten)
Das Ergebnis für jede Summe ist dann so etwas
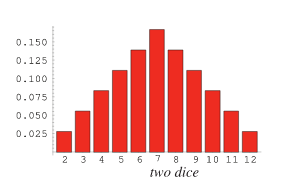
(Das ist die Formel die Bolthier meinte wie ich das verstanden habe, also für eine bestimmte Anzahl an Würfeln eine Summe)