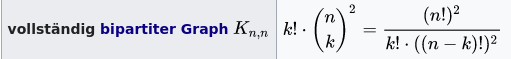In der Lösung sind zwei Fehler: Zum einen wird für E(M) in der Berechnung des Korrelationskoeffizienten 3,66 statt wie weiter oben ausgerechnet 3,88 verwendet, zum anderen werden die Varianzen verwendet statt korrekt die Quadratwurzeln der Varianzen.
was für ein Buch soll das sein
Pearson eignet sich eigentlich überhaupt nicht dafür
http://www.statistics4u.info/fundstat_eng/cc_corr_spearman.html
Calculating Pearson’s correlation coefficient requires the two samples to be linearly related and the scale of measurement has to be at the interval level. In the case of non-linear relations, Pearson’s correlation coefficient will lead to wrong results.
Beispiel für Noten für Weine, was ja dasselbe ist
Zudem wurde dieser auch noch falsch berechnet
Are you the one?
Ich hab mal wieder zu viel prokrastiniert.
Bei Are you the one muss man sein Perfekt Match finden und ab einen gewissen Punkt ist es ja Mathe.
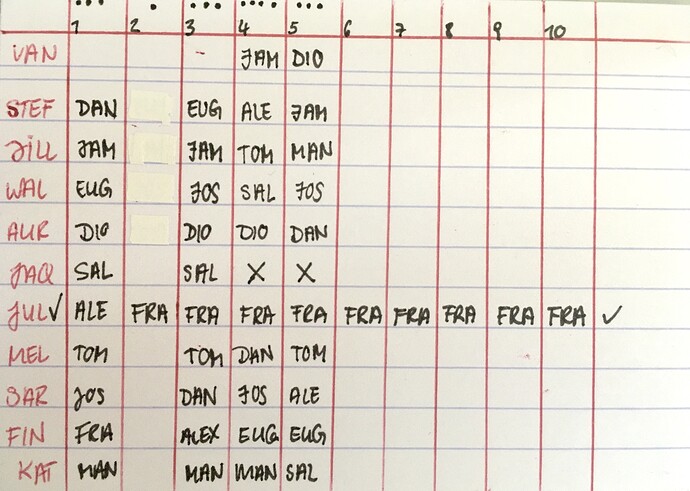
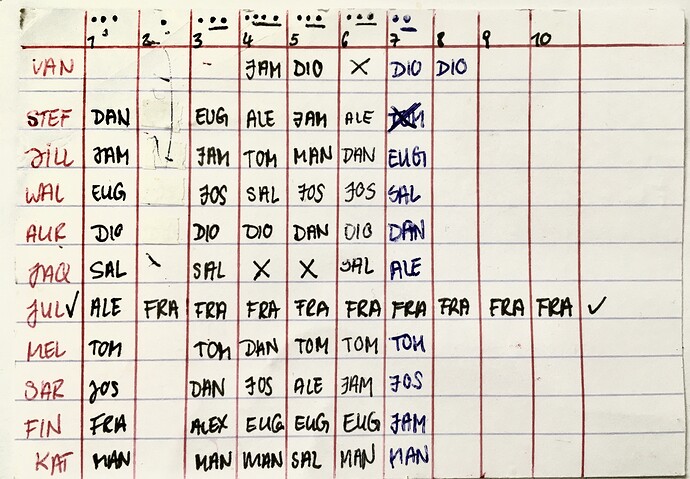
In 10 Nächten muss man sein Match finden oder man gewinnt kein Geld. Pro Nacht geht 1 Licht an, für ein Treffer, oder kein Licht für keinen Treffer (kleiner Punkt oben).
In der vierten Nacht kommt eine Frau hinzu (VAN rot). Ein Mann hat jetzt zwei Match Möglichkeiten.
Ein paar ist vorzeitig ausgezogen und wurde gelöst FRA + JUL.
WAL + TOM = ausgeschlossen
FIN + DAN = ausgeschlossen
Wie kann man jetzt die Chancen und Kombis berechnen?
Ein wenig konnte die Anzahl an Möglichkeiten verringert werden.
Und, meint ihr die Kandidaten könnten mit Mathe bis zur 10. Nacht lösen und wie würdet ihr in dem Spiel vorgehen?
Ich bin mir nicht sicher, ob ich alles verstanden habe, aber das Grundproblem sieht erst mal nach einem bipartiten Graphen aus und gesucht ist ein maximales oder ein perfektes Matching. Angenommen der Graph ist vollständig (WAL + TOM und FIN + DAN sind möglich), lässt sich die Anzahl möglicher Kombinationen (Matches) mit folgender Formel berechnen, wobei n = 10 ist (10 Frauen und 10 Männer) und k = 10 für die Anzahl an Matches die man sucht.
Dabei kommt raus, dass es 3 628 800 verschiedene Kombinationen an Matches gibt, was 10! entspricht.
Was ist jetzt mit Chancen gemeint und was genau ist in der Serie ein Match? Beziehungsweise, was muss eine Person machen, um zu gewinnen? Was weiß man und was weiß man nicht? 
Generell vereinfacht der bipartite Graph einige Probleme und da man ja Teil des Spiels ist, kann man die Unbekannten reduzieren.
Tja, das ist so die Sache, niemand kennt die Angaben oder Parameter (wie Kinderwunsch, im Berufsleben) usw., was für ein Match sprechen könnte. Das geht nach „Gefühl“.
In der Serie Daten sie sich, gehen dann in eine Box, wo es aufgelöst wird. Deswegen wissen wir, welche Paare wir ausschließen können.
Ich hätte gedacht, es gäbe jetzt Ausschlussverfahren. z.B. FIN - anhand der Lichter könnten wir DIO und MAN mal ausschließen (hypothetisch). Dann können wir DAN ausschließen, d.h. für FIN passen noch 7 Möglichkeiten.
Also über 3 Mio Möglichkeiten erscheint mir sehr komplex, dafür das sie am Ende gewinnen wollen.
Jeden Abend setzen sich die Paare zusammen und können anhand der Lichter nur mutmaßen wer passt, aber sie wissen das jemand passt! Deswegen find ich die vierte Nacht interessant.
Da sehen wir: AUR + DIO und KAT + MAN waren kontinuierlich bei Lichtern - und dann verlier ich schon den Faden… ![]()
Und an Tag vier hatten wir quasi die Hälfte an Treffern, 5 von 10 Paaren.
Geht tatsächlich einfacher
die Seite hatte ich auch schon gefunden, aber sie hat mir nichts gebracht
ich möchte ja jetzt durchgehen was stimmen könnte und bei ihm gings um Ausschlussverfahren?
Hinzu kommt noch Vanessa (VAN) und das uns eine Matching Night fehlt, plus das wir keinen Blackout hatten und das nicht sicher ist, welche drei Lichter ein Match sind.
Ich tippe auf AUR + DIO, KAT + MAN - die kontinuierlich gepaart waren. Aber in Nacht 5 haben wir auch Drei Lichter. Da würde ich dann AUR + DAN ausschließen und KAT + SAL, d.h. unter den restlichen sind drei Richtige wiederum.
Irgendwie dacht ich, es gibt ne Formel aus der Wahrscheinlichkeit oder so.
Ich würd sagen es fehlen uns noch ein paar die wir ausschließen können.
Ich kann mir nicht vorstellen, dass das Berechnen von Wahrscheinlichkeiten hierbei irgendetwas hilft, lasse mich aber gerne eines besseren Belehren 
Es ist eher ein Logikrätsel und ähnelt dem Spiel Mastermind. Durch Mustererkennung lassen sich Kombinationen ausschließen oder bestätigen. Aus den Kombinationen der 1. und 3. Nacht vermute ich, dass es in den 3 Kombinationen STEF-EUG, JOS-WAL und SAR-DAN höchstens 1 Match gibt. Das ist erst mal nicht so aussagekräftig, aber eine Regel die man sich zur Nutze machen kann.
EDIT: Ich bin jetzt richtig hooked und will die Lösung finden. Wenn die Paarungen der 6. Nacht feststehen, sag mir bitte Bescheid 
ja na dann, TV Now Abo!
haha, nein, ich vervollständige mein Karteikärtchen und lad es hoch
ich hatte auch den Gedanken!
man sieht ja auch KAT + MAN find ich irritieren, durch Nacht 5 - gehen wir davon aus, haben wir immer noch drei Lichter in Nacht 5
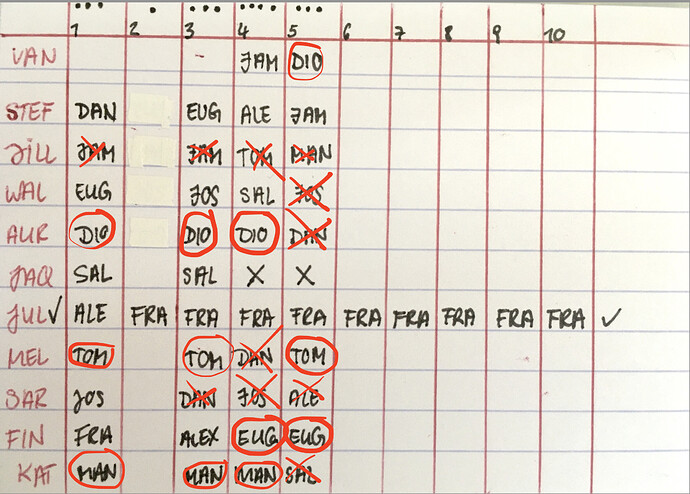
Das sind bisher meine Überlegungen, eingekreist sind Lichter
wobei JOS in Nacht 1 und 4 nicht klar ist, da TOM + MEL auch übereinstimmen
DIO + VAN + AUR (ein Mann hat zwei Treffer)
Gerade FIN ist spannend, weil wir hier schon DAN, FRA ausschließen können
und theoretisch DIO, TOM & MAN, bleiben noch EUG, JAM, ALE, SAL
Das Karteikärtchen der Liebe geht in eine neue Runde!
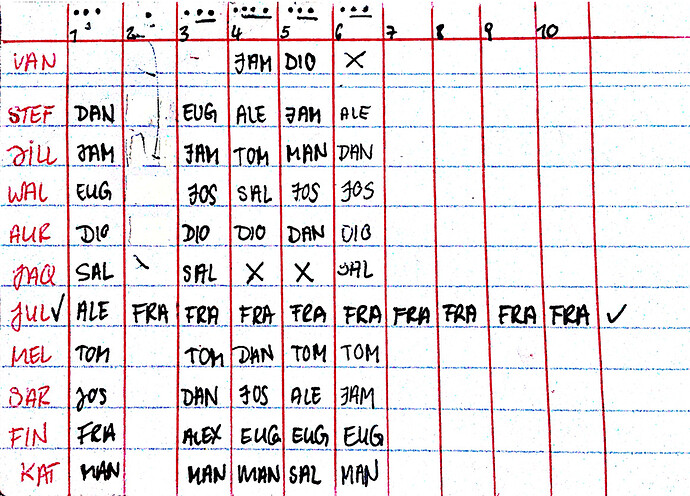
Ich hab auch einen Fehler gemacht. Ab Nacht 3 steht ein Punkt bereits für JUL + FRA. Ich habs irgendwie JUL + FRA plus drei Lichter. Das heißt, die stehen noch schlechter da als gedacht.
Folgende Erkenntnisse:
JUL = FRA
JUL ≠ ALE
WAL ≠ TOM
FIN ≠ DAN
FIN ≠ SAL
FIN ≠ FRA
Nacht 6, zwei Lichter plus JUL + FRA
Nicenstein!
Ahh, verstehe. Da JUL+FRA für jede Nacht weitergeführt wurde, bin ich einfach davon ausgegangen, dass sie zu den Lichtern gehören.
Ich hab ein kurzes Python Skript geschrieben, dass helfen soll alle möglichen Kombinationen an Perfect Matchings zu finden. Nach Nacht 5 waren es noch über 700, jetzt sind es nur noch 37. Sie könnten es also noch schaffen.
Und in 29 davon ist das Paar FIN+ALE vertreten. Also wenn sie herauszufinden könnten, ob die beiden ein perfektes Match sind, wäre das sehr von Vorteil
Also wenn man die Sendung so guckt, könnte ich noch welche ausschließen 
SAL + VAN zum Beispiel, aber man sollte sich ja nie zu sicher sein…
So, das Karteikärtchen der Liebe 
und die Gruppe verkackt total
neue Erkenntnisse:
FIN ≠ EUG (!)
FIN ≠ DAN
FIN ≠ SAL
FIN ≠ FRA
JUL = FRA
JUL ≠ ALE
WAL ≠ TOM
Eigentlich fast ein Blackout. (DIO bei 8 ignorieren, hab mich vertan)
Ich finde es sieht sehr stark nach KAT + MAN aus

glaubst du sie können noch gewinnen? @Boemi
Der FIN ≠ EUG Tipp kann noch viel wert sein. Als nächstes sollten sie KAT+MAN oder MEL+TOM testen. Wenn sie dabei ein Match finden, stehen die Chancen echt gut. Ansonsten habe ich eher das Gefühl, dass sie noch sehr im dunkeln tappen und deren Taktik nicht auf geht 
MEL & TOM geht nicht mehr, die Entscheidung haben sie verkauft 
die haben nicht so richtig eine Taktik, zumindest hat am Anfang eine Person nicht richtig mitgemacht und so ist halt auch die Stimmung der Gruppe… das kommt noch mal on Top, dann sind auch alle sehr überzeugt und festgefahren.
ALE will z.B. mal mit MEL matchen. Find ich gar nicht doof.
Aber ein Licht weniger und AUR + DIO sitzen nicht zusammen, das find ich interessant.
ein kleines weihnachtliches Matherätsel (nicht von mir)
44
ich stimme da völlig @RobChang zu.
Meist haben solche „Symbol-Gleichungssysteme“ ja auch noch so eine Irreführung dabei, dass irgendwo ein halbes Blatt fehlt oder eine Kugel mehr am Baum hängt…
…ist mir hier nicht aufgefallen - also einfach als lineares Gleichungssystem lösbar.
Die Lösung von @RobChang ist richtig.
Das schönste an dieser Aufgabe ist aber: Man könnte eine der drei vorgegebenen Gleichungen (nämlich die zweite) komplett streichen, und das Rätsel wäre noch immer eindeutig lösbar.
was ich gemacht hab